Dispersion naturelle d’aérosols, particules et polluants : le rôle des fluctuations turbulentes
Dispersion naturelle d’aérosols, particules et polluants : le rôle des fluctuations turbulentes
Dispersion naturelle d’aérosols, particules et polluants : le rôle des fluctuations turbulentes
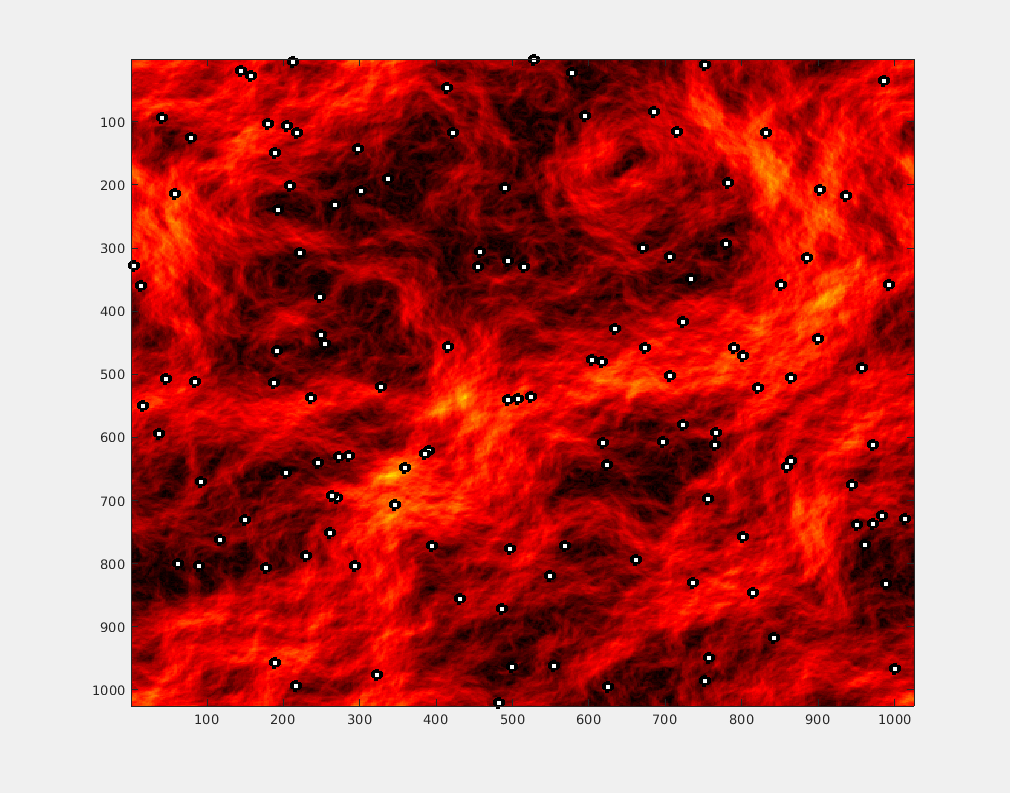
Simulation du mouvement de particules dans le fluide décrit par le champ aléatoire proposé dans ce projet. Les variations de couleur correspondent aux variations de la valeur du champ en fonction de la position. Les points représentent la position instantanée de particules évoluant dans ce champ.
Questions et outils mathématiques
Les chercheurs impliqués dans ce projet développent de nouveaux modèles stochastiques permettant de modéliser à la fois l’écoulement turbulent d’un fluide et le mouvement de particules se déplaçant dans ce fluide. Contrairement aux approches classiques, le fluide n’est pas décrit comme la solution d’une équation aux dérivées partielles de type Navier-Stokes, mais comme un champ aléatoire gaussien, qui évolue au cours du temps selon une dynamique stochastique forcée par un bruit blanc. Ce choix de modèle permet de reproduire certains aspects de la phénoménologie de la turbulence compatibles avec la structure gaussienne.
Premiers résultats et perspectives
Contrairement aux solutions d’équations aux dérivées partielles stochastiques usuelles, la solution de l’équation au cœur de ce nouveau modèle est régulière en temps, ce qui constitue un premier résultat d’intérêt. Un algorithme de simulation numérique efficace a également été proposé.
Dans un deuxième temps, le mouvement de particules est décrit et simulé à l’aide d’équations différentielles ordinaires ou stochastiques, dans lesquelles leur vitesse est calculée à partir de la valeur du champ aléatoire décrivant le fluide, et évaluée en la position de la particule à chaque instant. Les résultats de simulations du fluide et des particules sont comparés avec des simulations numériques directes et des expériences, afin de calibrer les paramètres et valider les modèles.
Ce projet implique trois physiciens de l’ENS Lyon (Mickaël Bourgoin, Laurent Chevillard et Romain Volk), un mathématicien de l’Université de Pau et des pays de l’Adour (Charles-Edouard Bréhier) et un doctorant en physique de l’ENS Lyon (Matthieu Chatelain).













