Modélisation des échelles sous-maille pour les modèles océaniques de climat
Modélisation des échelles sous-maille pour les modèles océaniques de climat
Modélisation des échelles sous-maille pour les modèles océaniques de climat
Dans le contexte du changement climatique, les modèles numériques du système terrestre sont des outils importants pour étudier la dynamique du climat et comprendre son évolution future. Le développement de tels modèles et de paramétrisations nécessite des interactions entre physiciens, mathématiciens, numériciens et informaticiens.
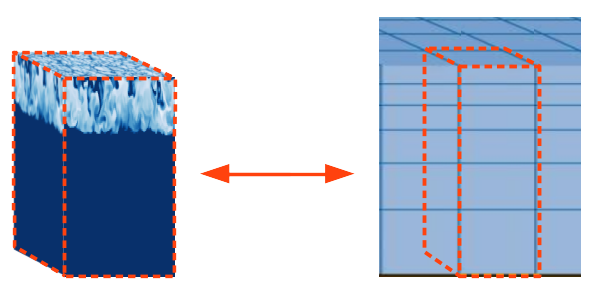
Représentation schématique du problème de paramétrisation. Une colonne verticale du modèle océanique est délimitée par les pointillés rouge (figure de droite). Les simulations LES à très haute résolution permettent une représentation explicite des processus d’intérêt à l’intérieur de cette colonne (figure de gauche). L’objectif est de rendre compte de l’effet moyen de ces processus sous-maille sur l’écoulement résolu par le modèle.
Questions et outils mathématiques
Pour des écoulements turbulents comme ceux de l’océan et de l’atmosphère, une représentation complète de toutes les échelles pertinentes est impossible à calculer avec la puissance de calcul actuellement disponible. Les modèles numériques intègrent ce que l’on appelle des paramétrisations pour tenir compte des processus clés trop petits pour être résolus par la grille de calcul. L’interaction entre ces paramétrisations et l’écoulement à grande échelle est un enjeu majeur pour garantir un niveau de réalisme satisfaisant des solutions numériques.
Dans ce projet, les chercheurs s’intéressent à la paramétrisation des panaches convectifs océaniques qui correspondent à des structures verticales cohérentes intermittentes dont l’échelle de longueur caractéristique dans la direction horizontale est bien inférieure à la résolution des grilles de calcul des modèles de climat.
Le problème de paramétrisation sous-maille d’intérêt se formule au niveau continu à l’aide d’une décomposition multi-fluide, parfois appelée multi-composante, entre un fluide « convectif » (modélisé par les équations de Navier-Stokes) immergé dans un « environnement » (modélisé par les équations primitives de l’océan). Une analyse dimensionnelle permet de simplifier la composante convective afin de rendre compte de son effet moyen via un système d’équations différentielles non linéaires dérivé sous des contraintes de cohérence au niveau énergétique et de prise en compte de l’échelle de la maille de calcul.
La formulation proposée fait intervenir des paramètres libres inconnus ou incertains sous la forme de coefficients ou de fonctions à calibrer. La suite de ces travaux s’intéressera aux méthodes de quantification d’incertitude et en particulier à l’estimation bayésienne de ces paramètres à partir de simulations à haute résolution, dites large eddy simulation (LES), résolvant explicitement les phénomènes convectifs.
Premiers résultats et perspectives
La démarche scientifique entreprise a permis une dérivation rigoureuse d’une paramétrisation de la convection dite en « flux de masse », ainsi que la réalisation d’un ensemble de simulations LES haute résolution de référence. Ces simulations permettront prochainement d’effectuer la calibration des différents paramètres intervenant dans le schéma en flux de masse. Une fois cette étape réalisée, la paramétrisation obtenue sera intégrée dans des modèles réalistes de l’océan, tels que CROCO et NEMO, pour en étudier l’impact sur la dynamique et la thermodynamique océanique.
Ce projet réunit des chercheurs en mathématiques appliquées, statistique, océanographie, météorologie, physique et modélisation numérique de l’océan et du climat. Il se structure essentiellement autour des travaux de thèse de Manolis Perrot, réalisés à l’Inria.
















